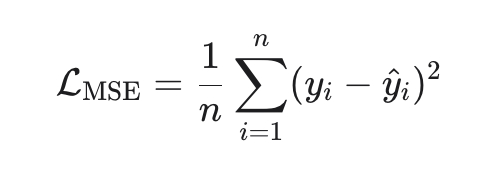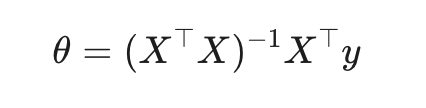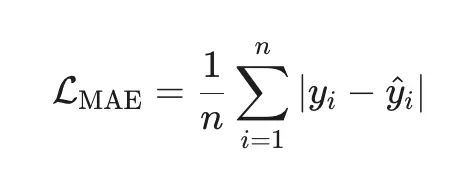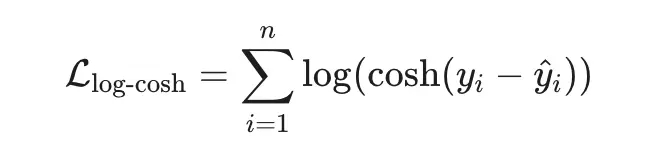Ответ на пост «Функции потерь и алгоритмы оптимизации в линейной регрессии: обзор основных подходов»1
Что такое функция потерь?
Что такое оптимизатор Adam?
Делаю такой клиповый курс «Что такое», где за 20 секунд объясняю термины по разработке нейросетей и искусственному интеллекту.
Если пост наберёт 30 плюсов, продолжу выкладывать другие клипы в сообществе «Наука | Научпоп».
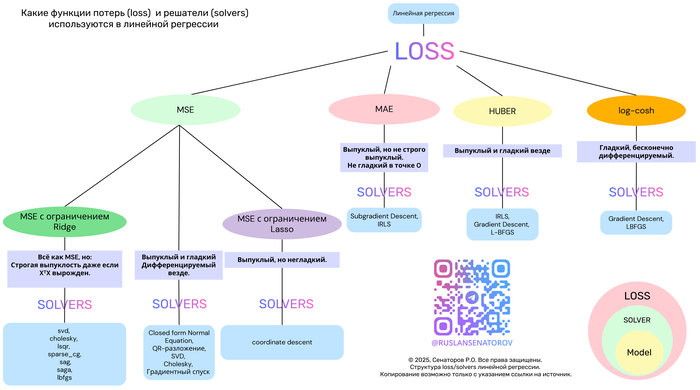
Функции потерь и алгоритмы оптимизации в линейной регрессии: обзор основных подходов1
Линейная регрессия — один из самых фундаментальных и широко применяемых методов в машинном обучении. Несмотря на простоту, её эффективность сильно зависит от двух ключевых компонентов:
Функции потерь (loss function) — что именно мы минимизируем?
Метода оптимизации (solver) — как мы ищем решение?
В этой статье мы разберём популярные функции потерь — MSE, MAE, Huber и Log-Cosh — их свойства, плюсы и минусы. А также покажем, как выбор функции потерь определяет выбор алгоритма оптимизации.
Почему функция потерь так важна?
Функция потерь измеряет, насколько предсказания модели отличаются от реальных значений. От её формы зависят:
Чувствительность к выбросам
Наличие замкнутого решения
Выпуклость задачи
Скорость и стабильность обучения
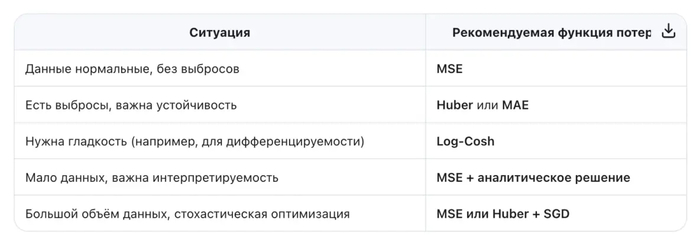
Давайте сравним четыре ключевые функции потерь в контексте линейной регрессии.
1. MSE (Mean Squared Error) — стандарт по умолчанию
Эквивалентна максимуму правдоподобия при нормальном шуме.
Замкнутое решение (метод наименьших квадратов):
Плюсы:
Выпуклая, гладкая, дифференцируемая → легко оптимизировать
Минусы:
Чувствительна к выбросам (ошибки возводятся в квадрат).
Solver:
Normal Equation (аналитическое решение)
SGD, SAG, LBFGS (в scikit-learn: solver='auto', 'svd', 'cholesky' и др.)
Когда использовать: когда данные «чистые», ошибки гауссовские, и важна интерпретируемость.
2. MAE (Mean Absolute Error) — робастная альтернатива
Плюсы:
Робастна к выбросам (ошибки в первой степени).
Минимизирует медиану ошибок (а не среднее).
Минусы:
Недифференцируема в нуле → нет аналитического решения.
Требует итеративных методов.
Solver:
Linear Programming (например, через симплекс-метод)
Subgradient Descent (в scikit-learn: QuantileRegressor с quantile=0.5)
Когда использовать: когда в данных есть аномалии или тяжёлые хвосты (например, цены, доходы).
3. Huber Loss — лучшее из двух миров
Плюсы:
Гладкая и дифференцируемая.
Робастна к выбросам (линейная штраф за большие ошибки).
Гибкость через параметр δδ.
Минусы:
Нужно настраивать δδ (часто выбирают как процентиль ошибок).
Нет замкнутого решения.
Solver:
Gradient Descent, LBFGS, Newton-CG(в scikit-learn: HuberRegressor с fit_intercept=True)
Когда использовать: когда вы подозреваете наличие выбросов, но хотите сохранить гладкость оптимизации.
4. Log-Cosh Loss — гладкая робастность
Плюсы:
Гладкая везде (бесконечно дифференцируема).
Ведёт себя как MSE при малых ошибках и как MAE при больших.
Устойчива к выбросам, но без «изломов».
Минусы:
Вычислительно дороже (логарифм и гиперболический косинус).
Не так распространена в классических библиотеках.
Solver:
Gradient-based методы: SGD, Adam, LBFGS(в TensorFlow/PyTorch легко реализуется; в scikit-learn — через кастомный регрессор)
Когда использовать:
когда вы ищете баланс между робастностью MSE и гладкостью MAE.
Вы хотите избежать чувствительности MSE к выбросам, но сохранить дифференцируемость.
Вы строите гибридную модель, где loss должен быть всюду гладким (например, для вторых производных).
Правило:
Если loss квадратичен → можно решить напрямую.
Если loss неквадратичен → нужен итеративный численный метод.
И помните: нет универсально «лучшей» функции потерь — только та, что лучше всего подходит вашим данным и задаче.
Решить пример: "6:2(1+2)=?;" или: "6:2а=?;" где: "а=(1+2);"
Прежде всего, нам необходимо оценить выражения: "2(1+2)"; и: "2а";
А). Одни утверждают, что между числом и скобкой, а также, между числом и буквой,- разрешается записывать знак умножения (точку), а можно точку и не записывать. Это считается одним и тем же выражением. Т. е. всегда соблюдаются тождества: "2(1+2)=2*(1+2)"; и: "2а=2*а";
Решение. По Правилу, решаем пример: слева, направо.
а). 6:2(1+2)=6:2*(1+2)=(6:2)*(1+2)=3*3=9;
б). 6:2а=6:2*а=(6:2)*а=3*а=(при: а=1+2)=3*(1+2)=3*3=9;
Б). Другие считают иначе. Точка не просто так опускается в таких выражениях. Если точка опущена, то это делается намеренно, чтобы показать, что: и: "2(1+2)"; и: "2а"; - это всегда ЕДИНЫЕ выражения. Тогда и решение получим другое:
а). 6:2(1+2)=6:(2+4)=6:6=1;
б). 6:2а=6:(2а)= (при: а=1+2)=6:[2(1+2)]=6:(2*3)=6:6=1;
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
Чтобы понять какое решение правильное, необходимо знать и четко различать принятые Стандарты написания тех или иных мат.выражений.
В большинстве стран Мира ( В том числе и в Р.Ф.) предписывается решать примеры со знаками дел. "двоеточие" и знаками умнож. "точка" строго слева, направо. Допускается, предварительно, выполнить операцию в скобках, - если это возможно сделать сразу. Но в данном "Правиле" никак не оговаривается, как требуется оценивать написание, или пропуск написания, точки в таких выражениях. Потому мы можем, как писать точку, так и не писать ее вовсе, - от этого значение выражения НЕ ИЗМЕНИТСЯ.
Вывод: Решение выражений по первому варианту (А) , считается, в названных странах, - правильным решением. То есть, это будут такие решения: "6:2(1+2)=9"; и: "6:2а=9"; при а=1+2;
,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
А другое замечание, что знак "точка" не просто так записывается или опускается в мат. выражениях, учитывается уже при оценке совершенно другого стандарта написания мат. выражения, в котором вместо знака "двоеточие" записан другой знак деления, а именно знак: "наклонная" черта. Поэтому сравните выражения:
а). 6/2(1+2)=6/(2+4)=6/6=1; Но уже: 6/2*(1+2)=(6/2)*(1+2)=3*3=9;
б). 6/2а=(при: а=1+2)=6/2(1+2)=6/6=1; Но уже: 6/2*а=(6/2)*а=3*а=(при: а=1+2)=3*(1+2)=3*3=9;
Данный факт мало кто учитывает при анализе решения данных выражений, а преподаватели в начальных классах их, фактически, упорно обходят своим вниманием.
Автор: А. Андреев. (13.12.2025 г.).
Как я узнала, что мои оценки по метаматике - ничто. Ноль без палочки
У меня в аттестате почти все 5, за редким исключением.
Я теперь даже не помню, по каким предметам было 4.
Но что удивительно- по математике и физике всегда было 5! Всегда.
Между тем, я ничего не смыслю в этих науках.
Те я хорошо решала уравнения, и даже графики к ним рисовала. Но никогда не понимала, что я делаю.
Просто была формула, был пример, как делать - я это усвоила - и просто повторяла.
Из школьной программы я вынесла - умножение/вычитание, сложение, дроби, проценты…. И это все!
Ну да, графики простые могу построить…
Пару лет назад в телеграмм канале наткнулась на энтузиаста, который , играючи, объяснил значение числа Пи.
Для меня это было открытием
И теперь я думаю, что мои преподаватели в школе тоже ни хрена не понимали.
Тоже, видимо, по шаблону работали
****
Хочу дополнить про химию.
В начале учебного года , когда только предмет ввели, я заболела. Недели две меня не было.
С тех пор я вообще не понимаю химию.
Хотя в аттестате 5. Не знаю, как так получилось.
Но! Мне хватило одного раза присутствия на уроке частного репитора, куда я отвела дочь.
О! Чудо! Женщина - препод начала с азов, и я сразу все поняла.
Ну вот как так?
И ещё- в Вузе - с горем пополам что-то сдала. Тоже не особо понимая.
Потом ещё получала ср.спец- там был классный препод. Она с меня три шкуры сняла, пока я сделаю так, как она хотела.
Но результат для меня лично - тот же + ноль.
Некорректное (на мой взгляд) условие задачи
Как вам такая задача?
Найдите наименьшее натуральное число, десятичная запись которого содержит все цифры от 0 до 5, и которое делится на все эти цифры (нуль не является натуральным числом).
Ссылка на источник задачи: https://mmmf.msu.ru/archive/20102011/z8/22.html
Если понимать буквально, то фраза «делится на все эти цифры» означает, что число делится и на 0. Но деление на 0 не определено вообще, ни для каких натуральных чисел.
Автор, правда, приписала: «нуль не является натуральным числом», но такая приписка не спасает положения. Формально она никак не отменяет того, что нуль всё ещё входит в список цифр, на которые делится число.
Или я чего-то не понимаю?