Карты

Мой первый рендер карты в Блендере. Классно или херня?

6144x4096

Если понравится, скоро выложу Европу и восточную Африку (а потом много чего еще!)

Источник: https://www.reddit.com/r/MapPorn/comments/gr7mrw/the_earth_b...

Карта с Новой Зеландией в центре:

Источник: https://www.reddit.com/r/MapPorn/comments/gqzk1h/the_earth_b...


Бонус:
Карта с Новой Зеландией посередине, но без Новой Зеландии

Источник: https://www.reddit.com/r/MapPorn/comments/gr65gw/this_map_ce...

1. Проекция Эккерта

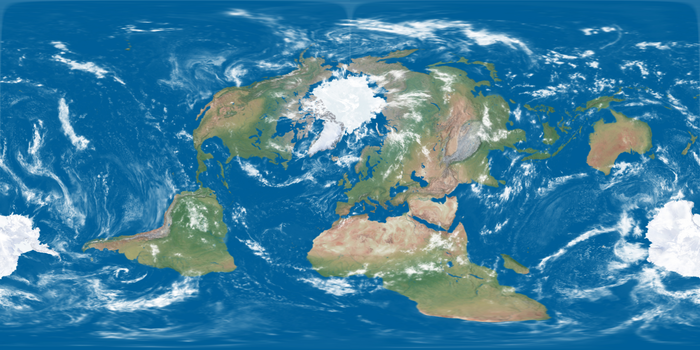
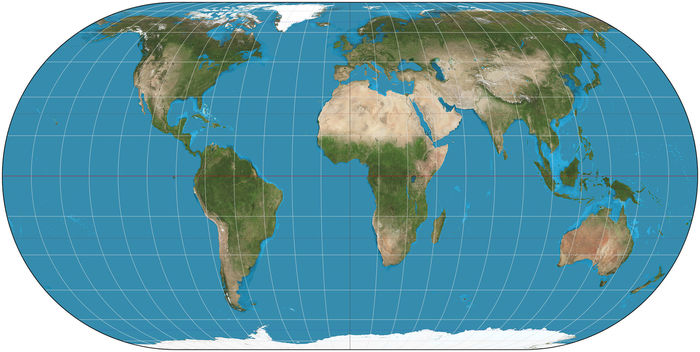
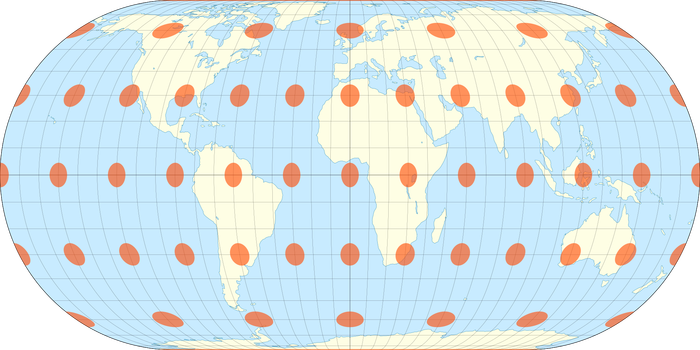
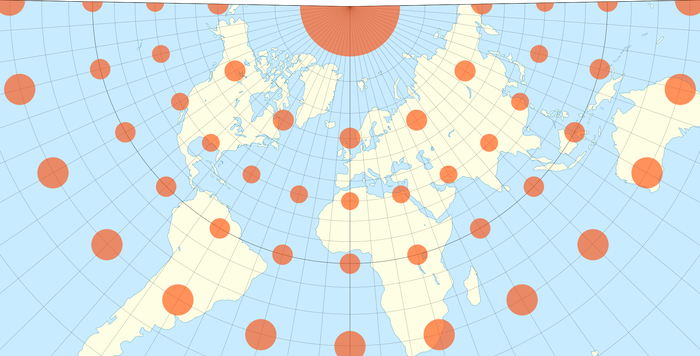
На самом деле их несколько. Представленная выше - это проекция Эккерта IV, сохраняющая площади (равновеликая). Ее стороны описывают полуокружности. Вот ее карта искажений:

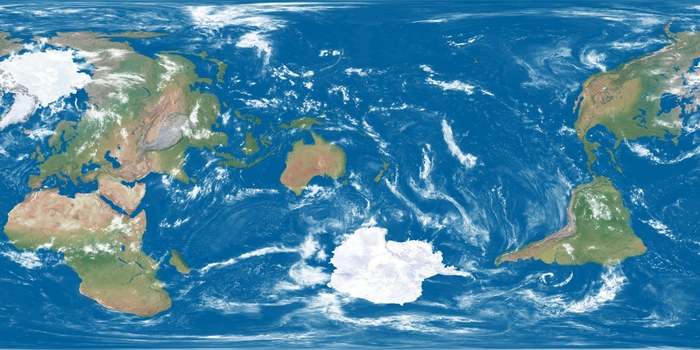
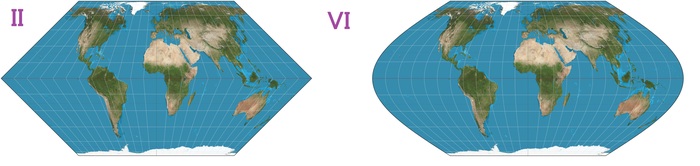
А вот ее II и VI подификации:

2. Проекция Гуда

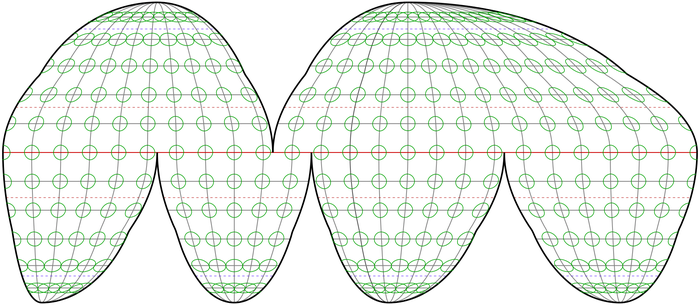
Равновеликая, псевдоцилиндрическая. Если кто-то спросит - гомолосинусоидальная. Разрывы позволяют уменьшить искажения форм стран, сохраняя пропорции по площади. А вот и искажения величин:

3. Проекция Каврайского

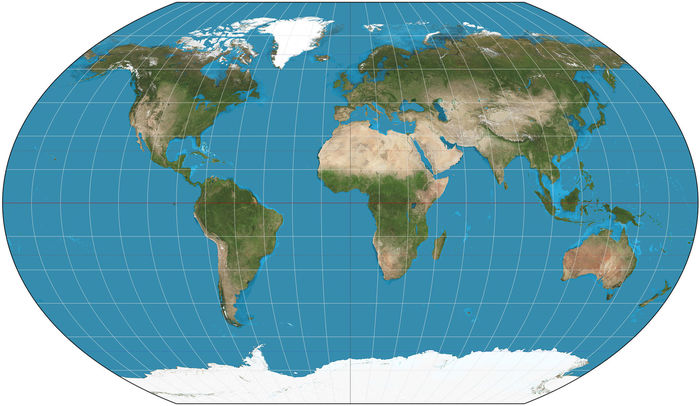
Эта карта неидеальна сразу по всем параметрам. В то же время, старается сбалансировать в себе и масштаб длин, и площадей, и формы стран, и целостность изображения. Так и называется: для общего назначения.

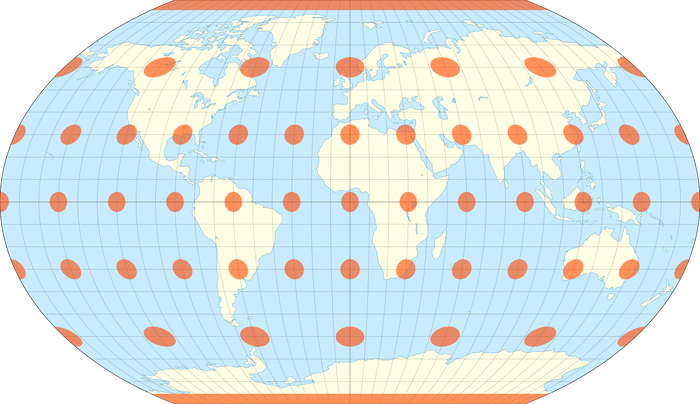
Искажения

4. Проекция Ламберта

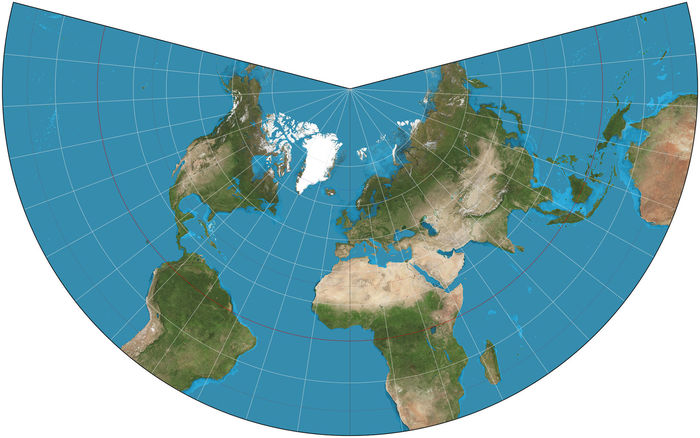
Собственно, это боковая поверхность конуса. То есть мы проецируем сферу на конус, а потом его разворачиваем. Славится достаточно точной передачей форм, особенно для средних широт, хотя ошибается в площадях.

Искажения:

5. Американская поликоническая проекция

В отличии от конической проекции Ламберта, это двойная коническая, как видно, и симметричная относительно экватора. Первая карта в посте (проекция Вернера) как раз основана на той же проекции Бонне, что и эта.

Впрочем, в плане сохранения масштабов длин у нее не очень:

6. Проекция Пирса

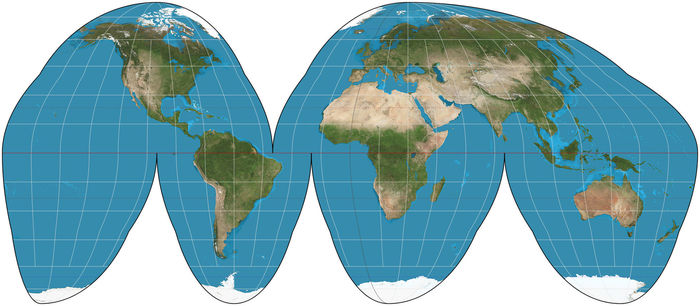
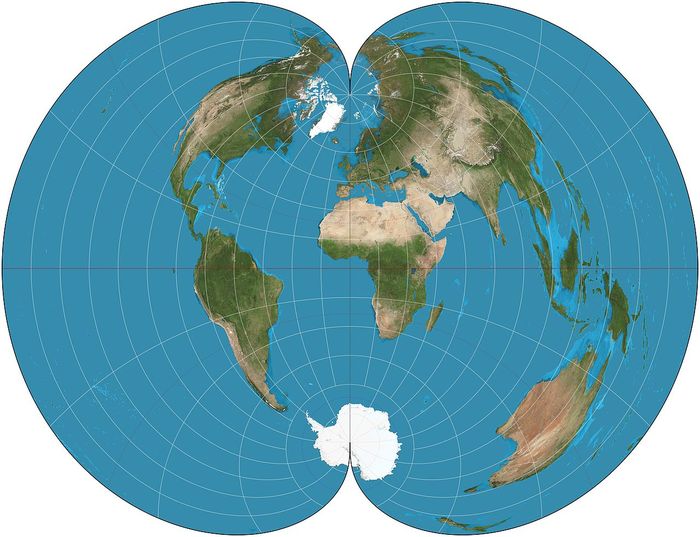
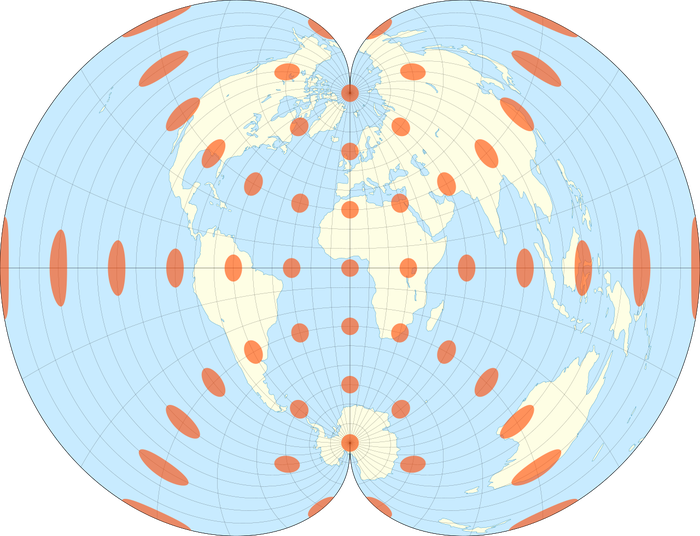
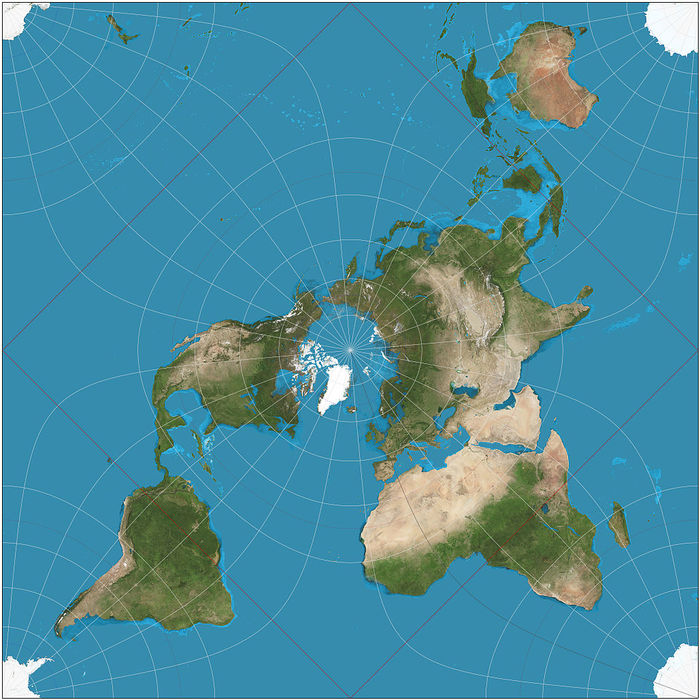
Суть в том, что эту можно соединять саму с собой сколько угодно раз, и она не сломается. Типа как плитка:

Правда, не особо-то ее часто используют. Разве что воздушные маршруты, что и сделали 70 лет назад.

Ее искажения:

7. Гномоническая проекция

Получается проецированием точек из сферы на плоскость. В разрезе это происходит так:

Эта штука вращается, описывая полный круг (сам нарисовал).

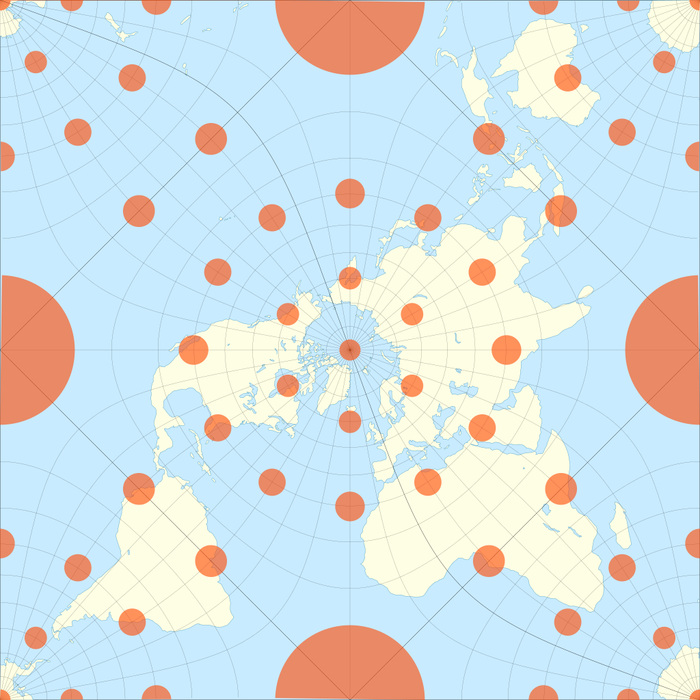
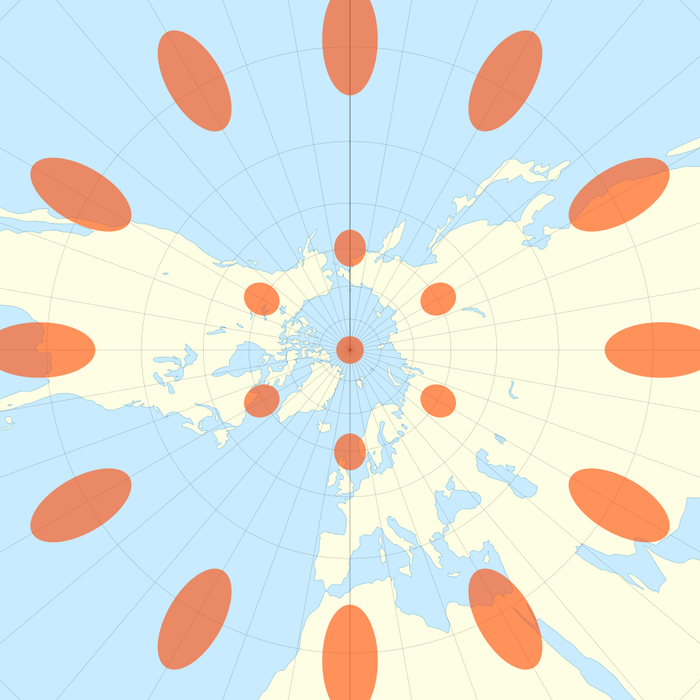
Сохранение точных масштабов - точно не сильная сторона гномонических проекций:

Так вот, столько разных проекций придумают для совершенно разных нужд. Какие-то актуальны внутри одной страны, какие-то нужны для построения маршрутов. Иногда важно сохранить длину вдоль меридианов, а иногда - критично сохранить отношение площадей.

Кажется, пока все.

Спасибо за внимание! Скоро будут еще карто-посты.

Источник 2017 года

Спасибо, что следите за постами сообщества.