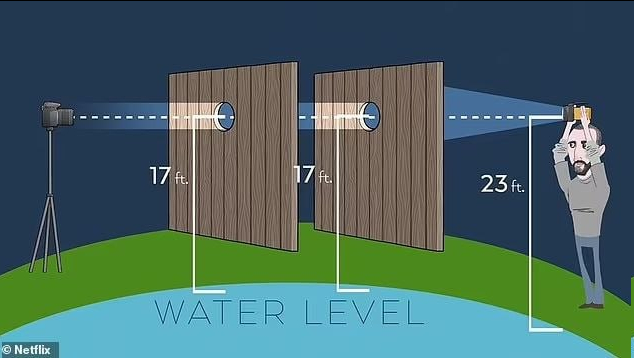
Ответ на пост «Сторонник плоской Земли потратил 20 тысяч долларов на эксперимент, доказавший, что планета всё же круглая»
А всего то надо замерить тень в 12:00 в разных локациях как было сделал Эратосфен (ок. 276–194 до н.э.).
В его ведении находилась великая Александрийская библиотека. Там он однажды обнаружил старый папирус, из которого узнал, что на юге, в Сиене, в полдень 21 июня вертикальный шест не отбрасывает тени. Эратосфен догадался поставить опыт в Александрии и проверить, отбрасывает ли вертикальный шест тень в полдень 21 июня. Оказалось, что отбрасывает.
Эратосфен задался вопросом, как получается, что в один и тот же момент в Сиене шест не отбрасывает тени, а в Александрии, которая находится значительно севернее, тень отчетливо видна. Эратосфен нашел этому лишь одно возможное объяснение: поверхность Земли искривлена. При этом чем больше кривизна, тем больше должна быть разница в длине теней. Солнце находится так далеко, что его лучи, приходящие на Землю, можно считать параллельными. Шесты, расположенные под разными углами по отношению к солнечным лучам, отбрасывают тени разной длины. Для того чтобы получить наблюдаемое различие между Александрией и Сиеной в длине тени, расстояние между ними по поверхности Земли должно составлять около семи градусов. Иначе говоря, если вы мысленно продолжите шесты до центра Земли, они пересекутся под углом семь градусов. Семь градусов — это примерно одна пятидесятая от трехсот шестидесяти градусов, составляющих полную окружность Земли. Эратосфен знал, что расстояние между Александрией и Сиеной составляло около 800 километров (он нанял человека, который шагами измерил дистанцию). Умножив 800 километров на 50, получим 40 000 километров — такой должна быть полная длина окружности Земли. Это правильный ответ.
Единственными инструментами Эратосфена были шесты, а еще — глаза, ноги и голова. Плюс любовь к эксперименту. И этого оказалось достаточно, чтобы определить длину окружности Земли с погрешностью в несколько процентов.