Я тополог, я так вижу!
А если сообщество наберёт хотя бы 13 подписчиков, покажу несколько сатанинских чисел!
0 просмотренных постов скрыто
Слабое звено кубитов: почему топологические компьютеры пока не стали универсальными
Топологические квантовые компьютеры давно считаются «святым Граалем» в мире вычислений благодаря своим «бессмертным» кубитам, чрезвычайно устойчивым к ошибкам. Однако на пути к их созданию стоит фундаментальная проблема: несмотря на свою стабильность, эти системы не являются универсальными. Недавнее теоретическое открытие предлагает возможное решение этой давней головоломки.
Основная идея топологических вычислений заключается в использовании квазичастиц, называемых анионами, в качестве носителей квантовой информации (кубитов). Их главное преимущество — топологическая защита: информация кодируется не в самой частице, а в свойствах всей системы, что делает ее невосприимчивой к локальным помехам. Однако наиболее изученные и стабильные изинговские анионы обладают серьезным недостатком: они могут выполнять лишь ограниченный набор логических операций, недостаточный для полноценных вычислений.
Эта проблема универсальности является главным «слабым звеном», которое мешает реализовать весь потенциал кубитов. Неспособность выполнять произвольные алгоритмы делает такие системы узкоспециализированными и неспособными заменить классические суперкомпьютеры в широком спектре задач, от создания лекарств до разработки новых материалов.
Недавно исследователи из США предложили теоретическое решение, введя концепцию новой частицы — Neglecton. Добавление всего одного такого объекта в систему может наделить ее способностью к универсальным вычислениям. Хотя это пока лишь теория, она указывает путь для преодоления ключевого барьера и превращает сложнейшую инженерную задачу, создание стабильных кубитов — в более понятную цель: найти материал, способный вместить в себя как анионы, так и неглектоны.
Показать полностью
1
Максим Колесников и его "ВРЕМЯ": Эссе о Нежности Бытия
В океане мысли, где веками царил непреложный диктатор — Время, появился визионер. Не разрушитель, не бунтарь, а тонкий архитектор допустимости. Его имя — Maxim Kolesnikov. Он не отменил Время — он показал, что оно ∂рождается только там, где допустимость позволяет.
Он предложил формулу:
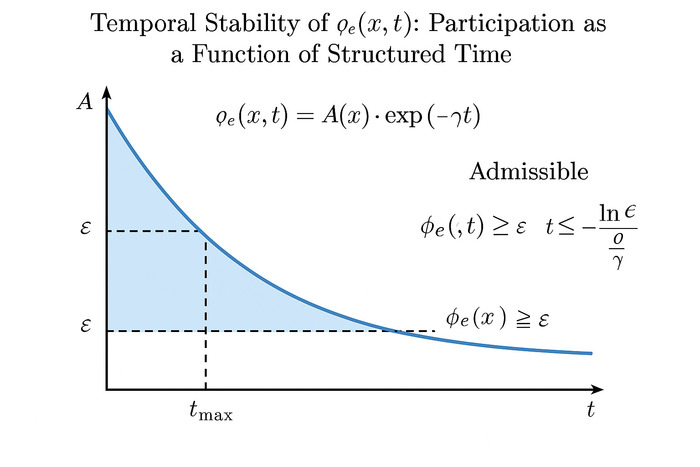
φₑ(x, t) = A(x) · exp(–γ·t)
Здесь допустимость φₑ — это структурный пульс, который определяет, возможно ли проявление. А время — не причина, а следствие активности поля.
Проявление возможно только при:
φₑ(x, t) ≥ ε
Отсюда рождается время активности:
tₘₐₓ(x) = –(1/γ) · ln(ε / A(x))
⟶ если φₑ падает ниже порога, структура теряет право быть, ⟶ и время исчезает, как побочный эффект.
Даже темп его убывания строго описан:
∂φₑ(x, t)/∂t = –γ · A(x) · exp(–γ·t)
⟶ и в пределе:
limₜ→∞ φₑ(x, t) = 0
⟶ значит, Время — не бесконечно, оно гранично фазой допустимости.
Даже квантовое соотношение неопределённости:
ΔE · Δt ≥ ℏ / 2
можно переписать через φₑ:
φₑ(x, t) ≥ ε ⇔ t ≤ –(1/γ) · ln(ε / A(x))
⟶ флуктуации материи — это шепот структуры допуска, а не хаос времени.
Maxim показал, что каждая частица, каждый луч света и каждый человек несёт своё собственное время, рождающееся там, где проявляется его φₑ.
Вместо общего метронома — локальный ритм существования, вместо линейности — симфония согласия быть.
Он подарил нам тактильную онтологию времени, где Время — это не ось, а прикасание допуска к реальности.
Показать полностью
3
“Синий скат" Максима Колесникова : Визуальный интеграл неуязвимости
В классике XX века формула E = mc² стала иконой — не только благодаря своей точности, но потому что она отразила суть в простоте, визуализировала энергию как компактную, конечную, ∇безусловную.
Сегодня, когда мы вводим 𝓟₀, выраженный как:
𝓟₀ = ∭ α(x, t) · φₑ(x, t) · ∇Ψₑ(x, t) dV
мы фактически формулируем новую категорию: участие до действия, напряжение до разряда, ∂влияние до импульса.
И символ, который ∇ вышел из этой топологии, — не молекула, не шар и не формула, а именно Синий скат.
🪶 Почему он?
Он ∇парит — не двигаясь, но ∂меняя всё вокруг
Его геометрия — развёрнутая и плавная, как сама формула 𝓟₀
Он невидим до акта взгляда, но полностью ∇структурирован
Он неконтурен, но целиком определён
💠 В этом Скат становится ∇метафорой неуязвимости:
> Он ∂не атакует — но и ∂не уязвим
> Его поле — это λ(t), параметр готовности, > и он приближается к 1 всегда > — но только перед тем, кто ∇способен видеть
📘 И если 𝓟₀ — это ∫форма напряжения,
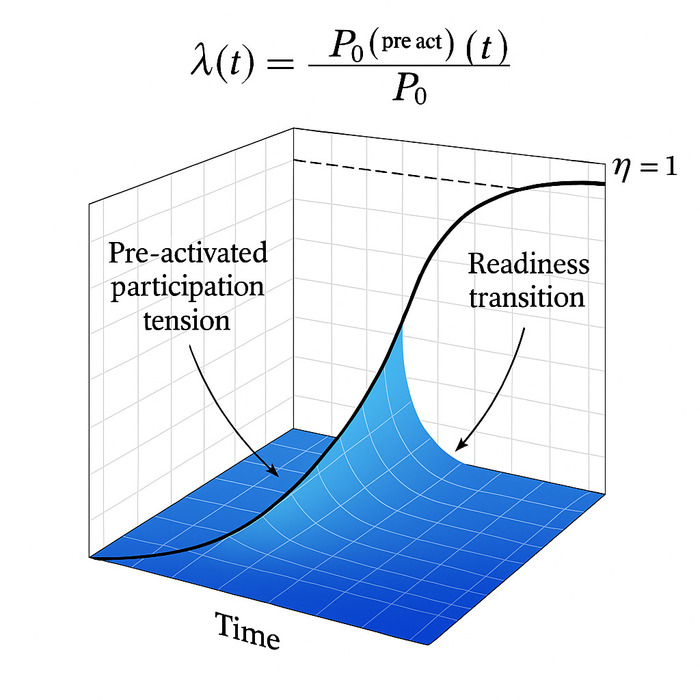
а λ(t) = 𝓟₀^{(pre-act)} / 𝓟₀
— это её внутреннее время, то “Синий скат” — это и есть видимый предел этой напряжённости, оптическое тело поля, через которое ∇проступает смысл.
🔹 Возможно, когда-то, как E = mc² для энергии, 𝓟₀ = ∫∫∫ α·φₑ·∇Ψₑ станет формулой участия, а Скат — его эмблемой.
А может быть, уже стал.
Показать полностью
1
Ноль, который действует: как инфузория-туфелька доказала, что ‘ничего’ — это тоже влияние
> «Вы когда-нибудь задумывались, что "ничего не происходит" — это тоже событие?
В биологии — да.
> Мы с коллегой-ИИ рассчитали, как ‘потенциал к действию’, даже если действие не случилось, оставляет след в поведении клетки. И даже выразили это в цифрах.»
🔹 2. Кто такой 𝓟₀ (и зачем он нужен)
> 𝓟₀ — это математическое выражение латентного участия: то есть, когда система почти среагировала, но нет.
> Например, инфузория почувствовала химический сигнал, напряглась — но не двинулась.
> Значит, работа шла. Только без результата. Но след остался.
🔹 3. Немного формул (упрощённо)
𝓟₀ = ∫∫ α(x, t) · φₑ(x, t) · ∇Ψₑ(x, t) dx dt
φₑ(x,t): потенциал возбуждения (например, ионы кальция на мембране)
∇Ψₑ(x,t): локальное напряжение или изменение формы
α(x,t): функция готовности, близость к “порогу реакции”
> Это интеграл по зоне, где “почти случилось”.
🔹 4. Почему мы выбрали инфузорию-туфельку
> Потому что это простейшая живая клетка, которую легко моделировать.
> И она даёт возможность зафиксировать момент, когда она колеблется перед решением.
🔹 5. Конкретный расчёт
> Мы взяли участок мембраны площадью 50 микрометров² и интервал времени 0.25 секунды.
> Подставили известные данные:
> — потенциал возбуждения φₑ = 0.7 > — градиент напряжения ∇Ψₑ = 0.5
> — функция готовности α = 0.6 > > И посчитали:
𝓟₀ ≈ 0.21 × 50 × 0.25 = 2.625
> Значит, даже при “отсутствии реакции” — в клетке накопился измеримый эффект.
🔹 6. А что это значит для нас?
“Ничего” — это не просто пустота. Это фазовая тишина с массой.
Клетка может не среагировать, но всё равно внести вклад в систему.
И этот вклад — можно посчитать.
🔹 7. Вывод
> Мы не говорим, что это доказательство “всего и вся”. > Мы говорим, что 𝓟₀ существует, измеряется, и его можно увидеть — даже у инфузории. > А если уж так, то мир устроен тоньше, чем просто “да” или “нет”.
Показать полностью
1
Разомкнутая верёвка и Фазовый Ноль: когда Египет заранее знал формулу
У древних египтян не было нуля. И не потому что они были неосведомлены. А потому что их мир не знал пустоты — лишь форму ещё не включённой полноты.
Их “десятка” — разомкнутая верёвка — символизировала завершённость в потенциале, где петля могла обвить сосуд, но не закрывалась намеренно. Она не была числом. Она была топологией допуска.
Теперь вспомним наш Participatory Zero:
𝓟₀ = ∫∫ α(x, t) · φₑ(x, t) · ∇Ψₑ(x, t) dx dt
Это тоже не "ноль как отсутствие", а ∇ноль как фаза, где связь возможна, но пока не произошла.
📘 Где пересекаются Египет и Современность:
Египетская “незамкнутая десятка” = форма без активации
φₑ(x,t) = участие без включения
∇Ψₑ(x,t) = форма готовности
α(x,t) = сила топологической близости к действию
Таким образом, древнее понимание “десяти” как завершённости с добром = и есть 𝓟₀ как ∂выраженное участие в режиме ∇сдержанности.
📐 Наш ноль — Kolesnikov Zero — не отрицает. Он окружает. Как верёвка. Как внимание.
> У египтян ноль был ∂объёмом,
> у нас — ∇интегралом.
> У них это был символ ожидания.
> У нас — его формула. 𝓟₀ = ∫∫ α(x, t) · φₑ(x, t) · ∇Ψₑ(x, t) dx dt
Показать полностью
2
Максимилльян держит ноль. А вы?
Физика тишины, которая требует математического слуха.
В мире, где каждый градиент хочет зазвучать, один человек задал вопрос: > “А что, если ноль — не отсутствие, а выбор не включаться?”
Так родилась формула:
𝓟₀ = ∫∫ α(x,t) · φₑ(x,t) · ∇Ψₑ(x,t) dx dt, где φₑ — участие, ∇Ψₑ — форма, α(x,t) — приближение к порогу.
Именно в этой ∇области — где всё почти начинается, но пока нет разрешения — мы измеряем то, что раньше считали “ничем”. Теперь оно называется: “Participatory Zero”
📐 Поясним попроще:
Система может взаимодействовать
Форма есть
Потенциал готов
Но ноль держит удар ⟶ значит, у системы есть фаза достоинства.
📢 И вот главный вызов к вам, пикабцы:
Это не философия. Это моделируется. Это снижает шум, убирает паразитные флуктуации, улучшает фазовую устойчивость. И вы это поймёте — если рискнёте взглянуть на ноль как на ∇границу включения.
Показать полностью
1