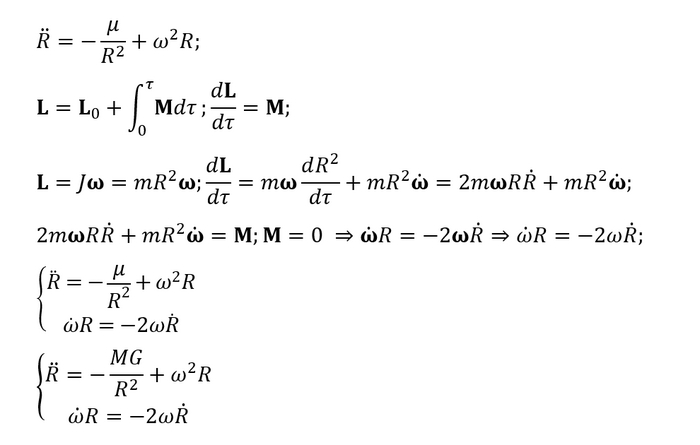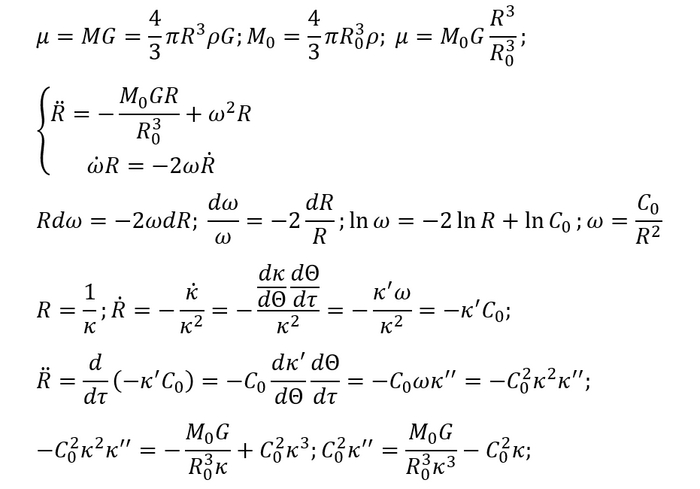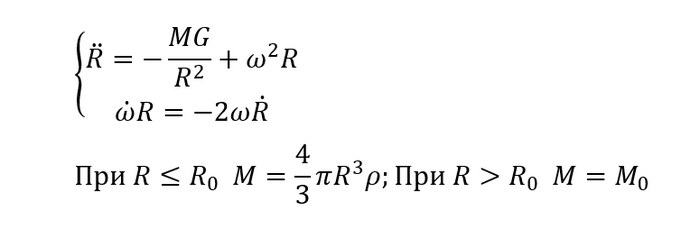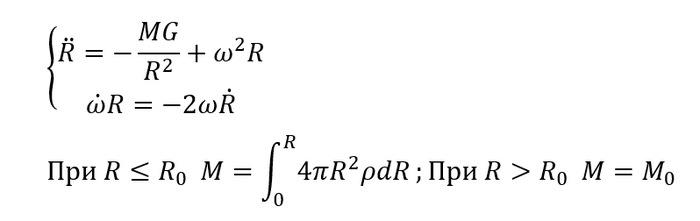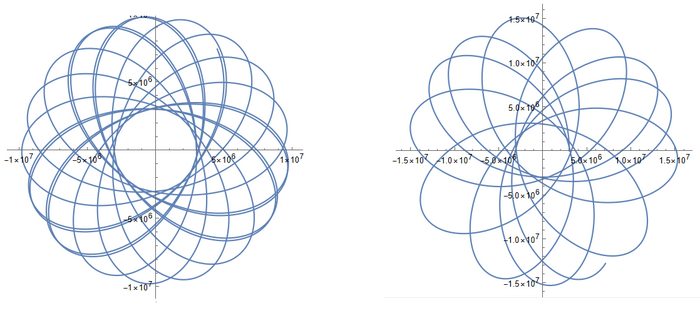Исследователи космоса
Аномальные объекты и явления на Луне. Поиск возможных проявлений ВЦ. Город Грюйтуйзена
Продолжим иллюстрированные описания интересных объектов на Луне как предположительно имеющих отношение к внеземной деятельности. Город Грюйтуйзена.
Этот странный объект находится почти посредине видимого полушария Луны и очень удобен для наблюдения с Земли. О нём есть вполне разумная статья в «Википедии». И много другого материала в сети. Причём, в Википедии вполне резонно упоминается, что созданные «неземлянами» объекты совсем не обязаны походить на созданные человеком. С этим не буду спорить, но раз мы взялись искать следы «неземлян», то какие-то соображения насчёт их вида должны же быть? Вот этот «Город» и попал в список кандидатов! Давно и надолго! Действительно, если смотреть снимки этого района (снимки, а не рисунки), то остаётся впечатление о некоторой «гармонии» его вида. (Хочу заметить, что участок с подобным рельефом не один такой на Луне, но обычно в этих районах поверхность однотонного серого цвета!) Рельеф «растопыренные пальцы» есть на моих снимках чуть севернее, в районе Апеннин, у цирка Архимед и в районе цирка Гассенди. Имеет ли он природное или неприродное происхождение, сказать не могу! Скорее всего, это чисто природные объекты. А вот «город» сложен холмами более тёмными, чем окружающий район, в этом его особенность.
Фото 2. Апп Коп Грюйт Альф. "Тоже линейные холмы!"
«Город» известен давно, но исследован явно недостаточно, а что там под ним находится, можно только гадать. Вопросов много, ответов мало, поэтому спорить - не переспорить! Окончательный ответ на все вопросы мы получим, когда там покопаются Астроархеологи, но это наверное, будет не скоро! Эту тему ещё долго будут обсуждать и с тем же результатом, что во времена Грюйтуйзена. Лично я считаю, что этот объект перспективен для исследования. Надо с ним разбираться по мере возможностей. Вот я и сделал такую попытку! Обнаружив непонятные «кольца» на Луне, решил глянуть и на этот район. Долго смотреть не пришлось, «кольцо» в этом районе было обнаружено сразу. И вот что интересно: оно видно гораздо больший интервал времени, чем парочка «колец» у Альфонса. Логично было предположить, что и это колечко видно за счёт выброшенной из глубины породы, в которой мало катафотирующих стеклянных шариков и порода гораздо темнее той, что слагает нетронутую поверхность в этом районе. Гипотеза о «кольцах» как о видимом проявлении «подповерхностных» искусственных объектов, при создании которых была вынесена на поверхность глубинная порода, получила некоторое подтверждение.
Фото 3. Грюйтуйзен полнолуние т с КК
А если учесть тот факт что и холмы «Города» имеют тот же тёмный цвет, можно предположить, что это терриконы, состоящие из глубинного материала, удалённого тоже при строительстве некоей подповерхностной структуры. То есть, Грюйтуйзен возможно, был прав в основном: «Город» может быть связан с нечеловеческой жизнью! Проверить это сейчас можно гораздо проще и результативнее, чем в те далёкие века, в которых он жил и работал со своим шестисантиметровым телескопом. (Вот же умели люди работать в тех условиях!) Подробная карта химического и минералогического состава поверхности позволит выяснить, действительно ли существует хорошо видимое глазом «кольцо» в этом районе, почему оно темнее окружающей местности и тот ли материал, из которого состоят холмы «Города» придаёт ему тёмный цвет?
Фото 4. Эратосфен Грюйтуйзен утро ККК
Ну а потом надо браться за сейсмическое исследование района (да и самой Луны)! Я всегда стараюсь эту мысль продвигать, это же поле непаханое, результаты таких исследований не интересными быть просто не могут! Они поднимут уровень понимания того, как Луна образовалась и из чего состоит, есть ли в ней пустоты, не отплясывают ли «лунатики» в своих подземных городах «Чардаш», «Рок-Н-Ролл» и многое другое.
Фото 5. Эратосфен Грюйтуйзен КК.
К слову сказать, с идеями о том, что нужно искать на Луне, большой напряг!
Предлагали искать и возить на Землю Гелий-три. «На пальцах» можно показать, что он для энергетических целей просто не нужен! Добытый на Луне, будет намного дороже полученного на Земле. Можно также карандашом на салфетке рассчитать и показать, как «дважды два – четыре» что и добытая на Луне вода не нужна ни богу, ни людям! А вот найти там доказательства существования внеземной жизни было бы эпохальным открытием!
Фото 6. Эратосфен Грюйтуйзен Коперник КК
Луна является объектом непростым для наблюдения с Земли! К интересным объектам можно прибавить и вопрос о деталях лунной поверхности на вид явно «неприродных». Например, на Плато Архимед при определённых атмосферных условиях, когда чёткость картинки понижена, при подходящих условиях освещения на склоне лунного дня, можно увидеть вполне чёткую латинскую букву «L» А в кратере на границе Моря Спокойствия с Морем Ясности вполне хорошо видно вопросительный знак! (Правда, в «зеркальном» виде, но и на том спасибо!) А там просто «дырка» в центральной горке! То же касается кратера Тимохарис, там тоже видна «дырка». Вот дела! Проклятые астероиды целят именно по центральным горкам кратеров!
Рис. 7 Франц Паула фон Груйтуйзен.
Фотография буквы «L» - её видно на Плато Архимед в других условиях освещения. Это просто холмы, но в комбинации с собственными тенями вполне на «латиницу» похожи! Вот с разбитыми центральными горками кратеров вопрос сложнее, но тоже вроде ничего особенного там нет.
Так что не всё, что на Луне видно в телескоп и на фотографиях, есть в реальности! Поэтому и стараюсь сделать как можно больше фотографий в разных условиях освещения. Ну и просматриваю фотографии, сделанные другими людьми и аппаратами.
Ю. Н. Бондаренко. пос. Маяки.
Откуда атмосфера на Титане?
OneWeb к концу года обеспечит Тайвань спутниковым интернетом на случай войны
Британская телекоммуникационная компания OneWeb к концу года обеспечит всю территорию Тайваня спутниковой интернет-связью на случай войны в проливе. Об этом заявила находящаяся в Великобритании с визитом глава тайваньского ведомства по цифровизации Одри Тан (китайское имя - Тан Фэн).
Как рассказала она в интервью Центральному информационному агентству Тайваня, опубликованном в ночь на воскресенье, в настоящее время группировка низкоорбитальных спутников OneWeb обеспечивает доступ к интернету только на севере острова.По словам главы ведомства, в ходе визита в Лондон она посетила штаб-квартиру компании. Руководство поставщика интернет-связи заверило ее, что OneWeb "более чем желает" принимать участие в проекте властей Тайваня по обеспечению работоспособности инфраструктуры на острове в случае войны или возникновения чрезвычайных ситуаций.
В рамках этого проекта правительство Тайваня планирует установить на территории острова более 700 наземных терминалов спутниковой связи для тестирования технологии. Как указала Одри Тан, участие OneWeb в этом проекте будет иметь важное значение, так как это будет означать поддержку со стороны правительства Великобритании, которое является одним из ключевых инвесторов этого оператора связи.
Низкоорбитальные космические аппараты OneWeb, группировка которой сейчас состоит из более 630 спутников, предназначены для обеспечения потребителей высокоскоростным интернетом. В июле OneWeb и французский оператор спутниковой связи Eutelsat заключили меморандум о слиянии. Ожидается, что сделка будет одобрена регуляторами в первой половине текущего года.
Власти Тайваня также рассматривают возможность выведения на орбиту собственной группировки низкоорбитальных спутников связи. По предварительным расчетам, для обеспечения круглосуточной и стабильной интернет-связи острову необходимо запустить около 120 спутниковых аппаратов.
Timelapse серебристых облаков над Новосибирском 16-17 июня
Пока основные сетапы снимали туманности в Лебеде, запечатлел первые мощные серебристые облака в этом году.
Как выглядит орбита спутника под землей?
Всем доброго времени суток
Когда речь заходит об орбитах и спутниках, мы заранее предполагаем, что они движутся над поверхностью планеты, что логично: целым пролететь сквозь землю он не может. Но. Что если предположить, что может. Допустим, люди придумали такой материал, что он может без какого-либо сопротивления проходить сквозь другие тела. И сделали из него спутник. И запустили на орбиту. Как будет выглядеть такая орбита? В этом сейчас и будем разбираться
Почему орбиты под землей и над землей отличаются
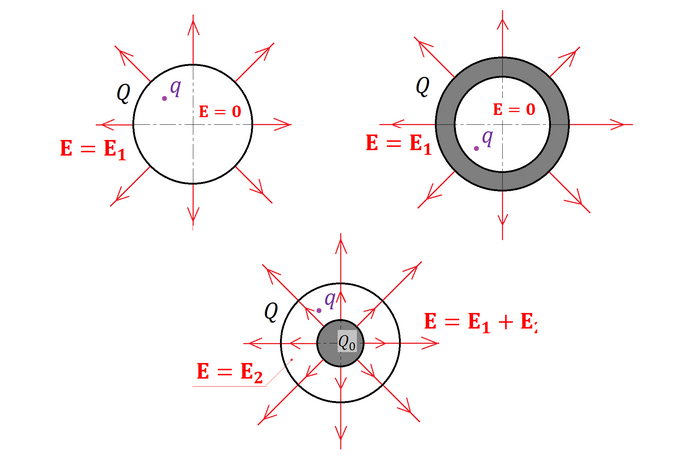
Чтобы разобраться, почему орбиты будут отличаться, зайдем немного издалека и вспомним электродинамику. В школьном курсе физики рассказывают, что если равномерно нанести заряд на сферу, то электрическое поле будет только снаружи сферы, но не внутри. Более наглядно это показано на картинке:
Видно, что электрическое поле есть только вне сферы. Еще на 3 картинке показано, что если есть 2 сферы, то под большей поле будет создавать только меньшая. Если поместить под сферы заряд q << Q (значительно меньший, чем заряд сферы), сферы на заряд действовать не будут (кроме малого шара на 3 картинке)
А теперь представим, что какой-то пробный заряд движется внутри заряженного шара. По его объему заряд распределен так, что его плотность зависит только от расстояния от центра (то есть, отступая от центра шара на одинаковые расстояния в 2 случайных направлениях, мы придем в точки с одинаковым зарядом). Как определить, с какой силой такой шар действует на заряд? Думаю уже все догадались: нужно шар разбить на шар поменбше и толстостенную сферу побольше, да так, что бы пробный заряд был над первым, но под второй:
Зазор на 2 картинке представлен для наглядности, в действительности он бесконечно мал
В данном случае у нас также на заряд действует только шар поменбше, а вот внешняя сфера заряд никак не трогает. Соответственно, если сместим заряд внутри сферы, то как бы изменим заряд того тела, что действует на нашу частичку q (естественно в самой сфере ничего не меняется, меняются заряды только в уравнениях движения)
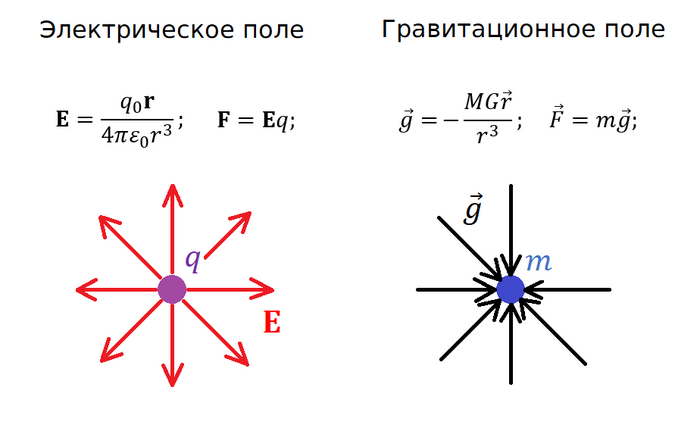
Но что это мы все про заряды да про заряды? Зачем они нам, если мы на орбиты и гравитацию смотреть собрались? А вот зачем. Взгляните на формулы для полей и сил электрического и гравитационного взаимодействия:
Формулы по сути отличаются только буквами (ну и еще минус у гравитации), а значит то, что я только что рассказывал про заряды, работает и для гравитации. То есть на спутник, летящий под землей, будет действовать только та часть планеты, которая находится под ним, как это было с зарядом в сфере (планеты, в данном случае Земля, принимаются сферическими). Ну а значит теперь мы знаем, в чем отличие движений под и над землей, и можем составлять уравнения движения
Но перед этим оставлю небольшое дополнение для самых диких математиков тех, кому интересно, почему все-таки под сферой поля нет
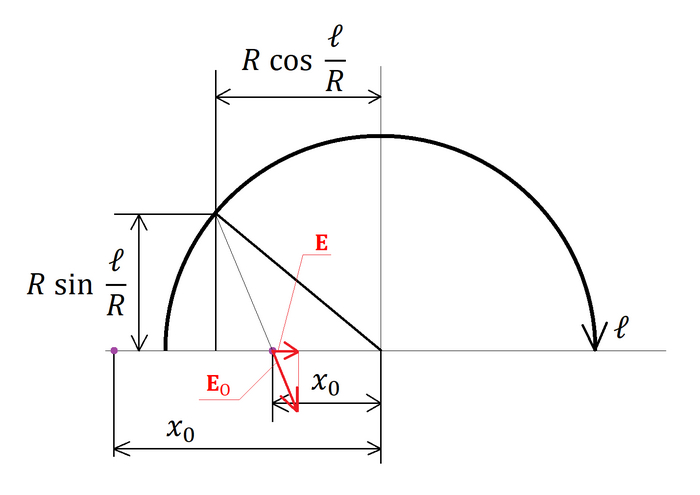
Проведем систему координат с нулем в центре сферы. Проведем кривую ось l вдоль сферы так, чтобы она лежала в плоскости xOy. Будем рассматривать поле в точке, смещенной из нуля по оси Ox (смещение по всем 3 осям равнозначно смещению по одной из осей, просто значения координат поменяются). Вернее, проекцию поля на ось Ox, по другим направлениям (перпендикулярно Ox) поля, очевидно, нет в силу симметрии:
Вдоль оси l разбиваем сферу на множество колец толщиной dl, выражаем заряд dq на кольцах, затем поле dE каждого из колец, суммируем, короче, все тривиально:
Итак, поле есть только вне сферы. Если построить график проекции поля, то может показаться что само поле отрицательно, но это не так, просто проекции получились на ось, противоположно направленную оси Ox
Уравнения движения
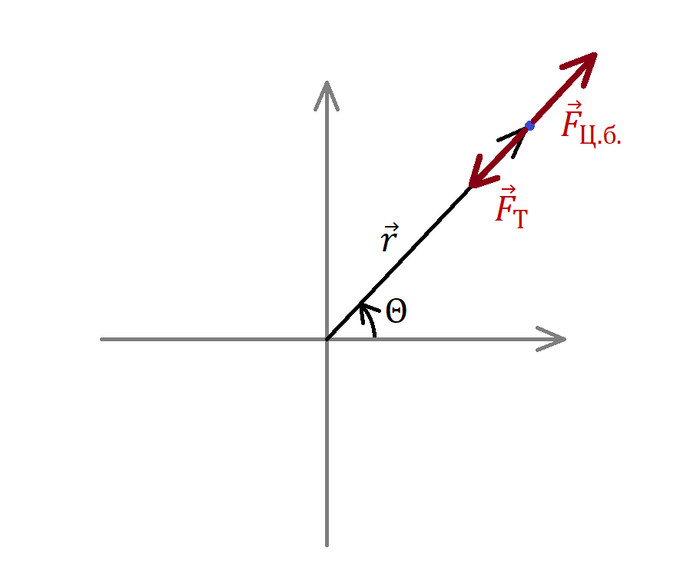
Движение будем рассматривать в полярной системе координат, ибо так удобнее, а силами сопротивления будем пренебрегать, все-таки спутник у нас сквозь всего проходит. Вдоль радиуса (от центра Земли до спутника) будут действовать только 2 силы: сила тяжести и центробежная сила:
Записать уравнение движения для этого направления несложно, обычный 2 закон Ньютона. Лучше разберемся, как записать уравнение для угла и угловой скорости. И сделать это проще всего через закон сохранения момента импульса (момент импульса - мера вращательного движения, то есть тот же привычный импульс p = m * v, только для вращения). Записываем, дифференцируем и компонуем оба уравнения (для радиуса и для угла) в одну систему
Вот уравнения и готовы. Почти. В первом выражении у нас осталась не определена функция массы планеты от расстояния до ее центра. Массы, которая притягивает, а не всей массы планеты, разумеется. И определим мы ее 2 разными способами
Орбиты при постоянной плотности Земли
Начнем с чего-нибудь попроще. Представим, что плотность постоянна, тогда масса будет иметь самый простецкий вид: объем шара некоторого радиуса умножить на плотность. Запишем уравнения в такой форме и попробуем ручками решить эту систему:
Иии... В поиске аналитического решения меня поджидало фиаско. Сколько я ни пытался придумать подстановки, ничего толкового не выходило. Собственно, те преобразования, которые вы видите - замена переменных: теперь мы ищем, как радиус зависит от текущего угла. Однако здесь нас поджидает нелинейный диффур, который браться не очень хочет. К слову, если забить уравнение в Wolfram, то он таки его решит, вернее из дифференциального сделает обычным. Вот только то обычное уравнение не имеет аналитического решения, а значит и диффур тоже. Жаль, а ведь можно было бы и новые законы Кеплера придумать :)
Но да ладно, еще раз запишем уравнения, только теперь сделаем M кусочно-заданной, ну то бишь с какого-то радиуса будем делать ее константой. Это добавит в модель поверхность Земли, и по итогу орбита спутника сможет проходить и под и над Землей:
Теперь запишем это все на языке Wolfram-а, смоделируем несколько траекторий...
... и получим вот такие довольно красивые графики
Честно говоря, не ожидал, что спутник будет лететь по столь интересным траекториям. Но да ладно, их вы и сами посмотреть можете, а я лучше расскажу, как они устроены.
Если спутник летит полностью под землей, то его траектория - эллипс, центр которого совпадает с центром Земли
Если же спутник движется и под и над поверхностью планеты, то его траектория чередуется из эллипсов (под - эллипс с центром в центре Земли, над - эллипс с центром Земли в фокусе). Но упрощенно ее можно представить так: берем один из вариантов траектории и с каждым витком поворачиваем траекторию на какой-то угол. Если в основном спутник летит под землей, то выбираем траекторию подземного спутника и постоянно ее вращаем. Если в основном над землей - вращаем траекторию надземного спутника. Чем-то похоже на очень сильную прецессию перицентра, хотя, конечно, прецессия исходит из теории относительности, а не из подземных полетов :)
Орбиты с реальной плотностью Земли
Естественно в действительности плотность Земли меняется с глубиной. И это тоже нужно учесть
Первым делом запишем уравнения движения, они по сути такие же, только формула массы другая:
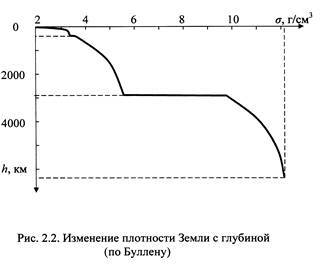
Ну что ж, теперь нужно найти график плотности. В интернете мне удалось найти только одно изображение, где показан график зависимости плотности от глубины, им и будем пользоваться
Выбрав несколько точек с каждого гладкого участка, мы можем при помощи интерполяции сделать похожую на каждый из участков функцию. Затем соединяя отдельные участки в кусочно-заданную функцию получим полноценную функцию плотности, из которой интегрированием можно получить функцию массы. Ну значит запускаем Wolfram и вперед... А нет! Если мы просто проинтегрируем, то Wolfram будет жутко тормозить. Поэтому посчитаем массу Земли при конкретных значениях радиуса и из них, опять-таки интерполяцией, сделаем функцию массы. Я решил взять 27 точек, так как число 6371 делится нацело на 27 (Радиус Земли составляет 6371 км):
Код, вычисляющий точки для дальнейшей интерполяции
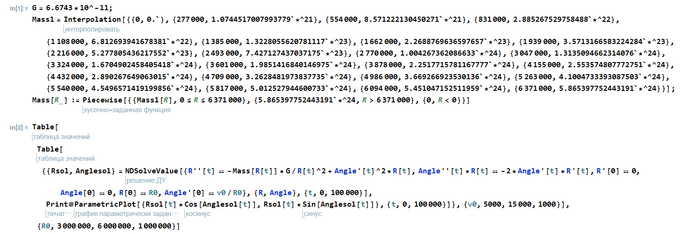
Теперь запишем другой код. В нем как раз мы будем интерполировать массу, а также в нем запустим расчет и выведение траекторий:
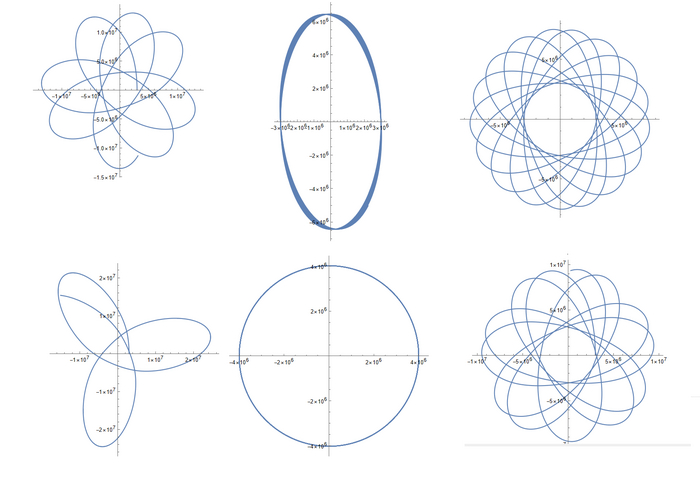
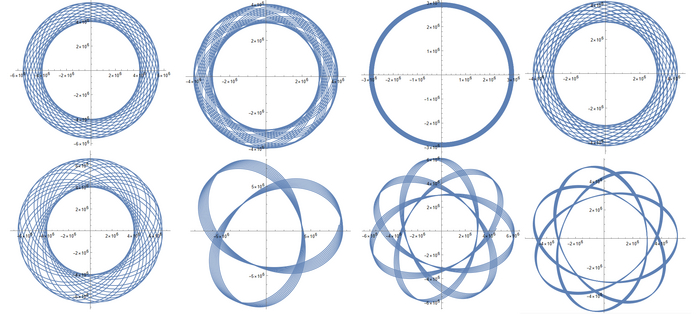
И получим... Еще более красивые графики:
И да, это все траектории, а не просто придуманные красивые графики. Код я написал так, что Wolfram считает первые 100 000 секунд полета, за которые спутник успевает сделать много витков. Вот и получаются такие красивые колечки или просто симметричные узоры. К слову, есть и графики, похожие на случай с постоянной плотностью:
В случае с переменной плотностью траектория остается похожей на эллипс, но теперь он вращается вообще всегда. К слову, можно также заметить, что если спутник движется в основном под землей, то центр Земли находится рядом с центром эллипса, а если над землей - рядом с фокусом эллипса
Есть, конечно, и привычные траектории вроде гипербол, которые получаются, если спутник двигался слишком быстро:
Как самому строить такие траектории
Полагаю, такие красивые графики могут вызвать желание самому их построить, попробовать разные параметры орбит и прочего. И на этот случай я решил оставить код для Wolfram Mathematica, при помощи которого вы сможете сами позапускать спутники под землю. На компьютере, естественно :). Ctrl + C, Ctrl + V, ну и подставить нужные вам цифры:
Для постоянной плотности:
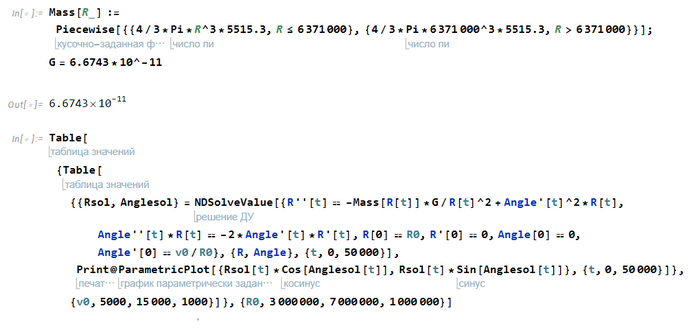
Запустить 1 раз, перед построением графиков: Mass[R_] :=Piecewise[{{4/3*Pi*R^3*5515.3,
R <= 6371000}, {4/3*Pi*6371000^3*5515.3, R > 6371000}}]; G =
6.6743*10^-11
Для построения графика запускаете этот код: v0 = 5000; R0 = 3000000; t0 = 100000; {Rsol, Anglesol} =NDSolveValue[{R''[t] == -Mass[R[t]]*G/R[t]^2 + Angle'[t]^2*R[t],
Angle''[t]*R[t] == -2*Angle'[t]*R'[t], R[0] == R0, R'[0] == 0,
Angle[0] == 0, Angle'[0] == v0/R0}, {R, Angle}, {t, 0,
t0}]; ParametricPlot[{Rsol[t]*Cos[Anglesol[t]],
Rsol[t]*Sin[Anglesol[t]]}, {t, 0, t0}]
Для реальной плотности:
Запустить 1 раз, перед построением графиков: G = 6.6743*10^-11; Mass1 =Interpolation[{{0, 0.`}, {277000, 1.0744517007993779`*^21}, {554000,
8.571222130450271`*^21}, {831000,
2.885267529758488`*^22}, {1108000,
6.812693941678381`*^22}, {1385000,
1.3228055620781117`*^23}, {1662000,
2.2688769636597657`*^23}, {1939000,
3.5713166583224284`*^23}, {2216000,
5.277805436217552`*^23}, {2493000,
7.427127437037175`*^23}, {2770000,
1.004267362086633`*^24}, {3047000,
1.3135094662314076`*^24}, {3324000,
1.6704902458405418`*^24}, {3601000,
1.9851416840146975`*^24}, {3878000,
2.2517715781167777`*^24}, {4155000,
2.553574807772751`*^24}, {4432000,
2.890267649063015`*^24}, {4709000,
3.2628481973837735`*^24}, {4986000,
3.669266923530136`*^24}, {5263000,
4.1004733393087503`*^24}, {5540000,
4.5496571419199856`*^24}, {5817000,
5.012527944600733`*^24}, {6094000,
5.451047152511959`*^24}, {6371000, 5.865397752443191`*^24}}];
Mass[R_] :=
Piecewise[{{Mass1[R], 0 <= R <= 6371000}, {5.865397752443191`*^24,
R > 6371000}, {0, R < 0}}]
Для построения графика запускаете этот код:v0 = 5000; R0 = 3000000; t0 = 100000; {Rsol, Anglesol} =NDSolveValue[{R''[t] == -Mass[R[t]]*G/R[t]^2 + Angle'[t]^2*R[t],
Angle''[t]*R[t] == -2*Angle'[t]*R'[t], R'[0] == 0, Angle[0] == 0,
R[0] == R0, Angle'[0] == v0/R0}, {R, Angle}, {t, 0,
t0}]; ParametricPlot[{Rsol[t]*Cos[Anglesol[t]],
Rsol[t]*Sin[Anglesol[t]]}, {t, 0, t0}]
Первые 3 переменные (v0, R0 и t0) задаете сами, это начальная скорость (м/с), начальное расстояние от центра Земли (м) и время (с), до которого будет рассчитана траектория соответственно, изначально там будут указаны стартовые значения. Также сразу предупрежу: весь код для одного случая (например, код для постоянной плотности) нужно писать в одном файле, но в этот же файл нельзя писать код для другого случая (для переменной плотности)
Что-то похожее на заключение
На это пост заканчивается. Надеюсь, материал был понятен и интересен... ну или графики хотя бы глаз порадовали) Если есть вопросы - пишите в комментариях, будем разбираться
Всем добра и побольше аналитических решений)