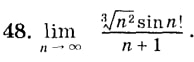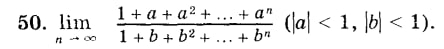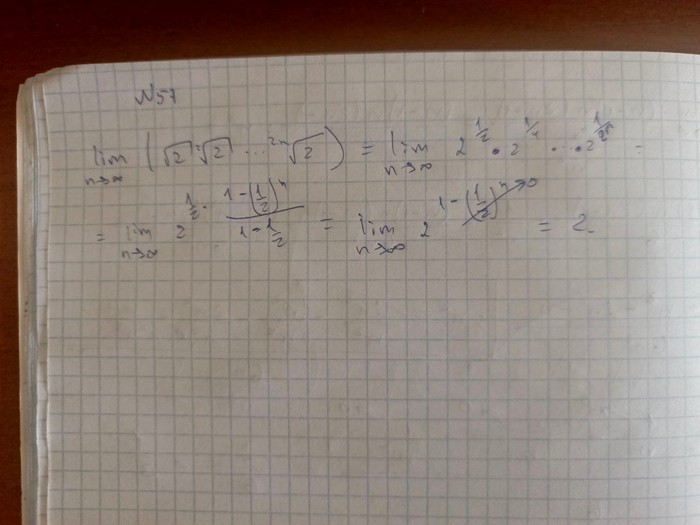Ответ на пост «Отмечать светофоры - прошлый век. Китайская капча предлагает очистить кошачий лоток»4
А что если на место капчи подставлять какие-нибудь олимпиадные задачи? Решить дифур или интеграл?
Матановая капча
Якобы такой пароль просили в студенческой столовой в Китае.
На самом деле этот интеграл решается 11-классником едва ли не устно.
Поехали?
С симметричной областью интегрирования проверим чётность функций.
Первое слагаемое нечётно и даёт интеграл, равный нулю. Остаётся вот что.
Нарисуем интеграл графически.
Перед нами четвертушка круга с радиусом 2.
1/4·π·2² = π
Таким образом, пароль — всего-навсего 31415926.
Пароль, конечно, не очень удачный (с правильным округлением будет …927), но большинство калькуляторов дают именно такое приближение числа пи.
Остаётся узнать, кто первый узнал восемь цифр числа пи. Википедия говорит, что это Цзу Чунчжи, который около 480 года показал, что пи — это 3,1415926+.
Вот вариант с YouTube.
Сказка о Нутаке и Бесконечно Остром Лезвии
В яранге выло, словно сам дух зимы рвался внутрь. Не холод был, а сам Эргы-Кэле, Дух Всесокрушающего Холода, дышал за оленьей шкурой входа, и лёд сковывал землю.
Нутак вскочил, схватил своё копьё с наконечником из крепчайшего рога.
— Пойду! Найду его логово! Сокрушу его!
Ы’трин не шевельнулась. Сидела, словно камень у жировой лампы. Сказала, не глядя:
— Его суть — вечный лёд. Он не из плоти. Твоё копьё ударит и отскочит, как от скалы. Не взять его силой.
— Всё можно сокрушить, если бить сильнее! — упрямо возразил Нутак.
— Сила? — Ы’трин медленно повернула к нему голову. Её взгляд упал на потолок яранги, где висели длинные, крепкие сосульки, намерзшие от дыхания спящих. — Смотри.
Она взяла его самое крепкое копьё и легонько ткнула им в толстое основание сосульки. Острый наконечник скользнул по гладкому льду, оставив лишь белую царапину, и соскользнул в сторону.
— Видишь? — сказала Ы’трин. — Лёд твёрдый и гладкий. Чтобы его победить, нужно не бить сильнее. Нужно не ударить по нему, а коснуться его сути. Нужно лезвие, которое соберет всю силу мира в острие, тоньше иглы. Чтобы на его кончике родилось Йыгыргын Ы’мыл Бесконечное Сжатие, что плавит лёд самого бытия.
— Где взять такое? — выдохнул Нутак, наглядно поняв тщетность грубой силы.
— Не взять. Сделать, — сказала шаманка. Она достала старый нож и точильный камень. — Точи. Но не как обычно. Точи по Пув’эт Вэтгав Ы’мылгыльын — По Пути-Закону Всеведающего. На этом камне, что зовётся Йыргыр («Превращатель»).
— Какому закону?
— Сначала убери половину толщины лезвия.
Нутак провёл раз, другой. Нож стал немного тоньше.
— Теперь — половину от той толщины, что осталась.
Нутак сделал.
— Теперь — снова половину от того, что теперь осталось.
Нутак водил ножом по Йыргыр. С каждым разом лезвие становилось всё тоньше. Тоньше крыла мошки. Тоньше паутинки. Но он видел — край всё ещё был.
— Я никогда не закончу! — воскрикнул он. — Всегда остаётся ещё хоть немного!
— Так, — кивнула Ы’трин. — Для счёта движений — не закончишь никогда. Движений будет больше, чем снежинок в пургу. Но посмотри на лезвие. — Она подняла его против слабого света жировой лампы. — Оно уже тоньше, чем дыхание духа. Тоньше, чем может увидеть глаз. Ты не сделал его бесконечно тонким. Но ты сделал его таким, что разница не имеет имени. Теперь это не просто нож. Теперь это Вынгэ («Проникающий»). На его острие теперь рождается Йыгыргын Ы’мыл — та самая сила, что сжимает мир до точки. Это и есть Вэтгав Ы’мылгыльын. Лезвие не стало идеальным, но для Эргы-Кэле оно теперь опаснее самого жара солнца.
Молчал Нутак. Держал в руках Вынгэ, что почти невесом.
— Значит, я не убью его, но я раню его?
— Так, — сказала Ы’трин. — Силы на это хватит.
Вышел Нутак навстречу стуже. Эргы-Кэле был подобен движущейся горе изо льда. Нутак бросился вперёд и не стал бить, а лишь коснулся ледяного сердца духа своим Вынгэ.
Клинок не сломался. Он не пронзил лёд, как пронзают плоть. Он вошёл в него, как свет входит в воду. В точке касания вспыхнула крошечная звезда — Йыгыргын Ы’мыл зажглось, и сердцевина холода треснула изнутри с тихим стоном.
Раздался хруст, словно лопнула тысяча льдин. Эргы-Кэле издал тихий, подобный ветру вздох и рассыпался на мириады сверкающих пылинок, что унесло ветром.
Вернулся Нутак в ярангу. Стужа отступила. Огонь в очаге затрещал веселее.
Ы’трин глядела на пламя, сказала:
— Куркыль не просто мир создал. Он законы сплёл. Даже бесконечную силу сделал конечной в руках того, кто понимает.
Белый шум, красный шум, розовый шум, CS2, DFA
Почему случайные люди, собранные случайным образом в команду выигрывают, а другие проигрывают. На примере игры Counter Strike.
«Мы пять лосей собрались в CS — и выиграли катку. А в другой раз — пять звёзд — и слили за 15 минут. Как так?»
Сейчас расскажу про белый, розовый и красный шум.
Сначала про «цветные шумы»
Вы слышали про белый шум? Это когда советуют: «Засыпай под дождь и шум моря»
Технически — это случайный сигнал, где всё частоты одинаковые. Никакой связи между моментами. Просто ХАОС.
Потом есть розовый шум — да, такой реально существует.
Он менее резкий, более «естественный». Так звучит сердце, волны, ветер в лесу, хороший трек или… работающая команда в КС.
Его ещё называют 1/f-шум — мощность падает с ростом частоты. Но главное — он живой, гибкий, гармоничный.
И да, есть ещё красный шум.
Он вообще почти все низкие частоты — медленный, инертный. Как будто кто-то сказал:
«Ну мы же всегда так делали, зачем менять?»
→ Это когда команда играет один план 10 раундов подряд, даже если он не работает.
А теперь — к Counter-Strike
Представьте:
Собрались пять человек. Никто не pro, все с работы/учебы, зашли поиграть.
Никто не кричит, никто не тилтует.
Один сказал: «Рашим Б», все пошли.
Проиграли — сказали: «Ок, в следующий раз А».
И начали выигрывать.
А рядом — команда с двумя про, один с aim как бог, другой читает карту наизусть.
Но:
Все хотят быть капитаном.
Один кричит: «Я иду А!» — а сам идёт Б.
После поражения: «Это ты виноват! Я бы взял, если б ты не стоял как турель!»
И что вы думаете?
Первая команда выигрывает. Вторая — сливает.
Почему?
Потому что первая команда — это розовый шум.
Их действия связаны, но не жёстко. Есть ритм. Есть память. Есть адаптация.
Как музыка — не хаос, не монотонность, а гармония.
А вторая — белый шум: каждый сам по себе, никакой согласованности.
Шум, крик, беспорядок → проигрыш.
А если бы они вообще ничего не меняли, играли один план — это был бы красный шум: слишком много стратегии, слишком мало мозгов.
DFA
Есть такой научный метод — DFA (Detrended Fluctuation Analysis).
Не пугайтесь, это просто способ понять, насколько поведение системы предсказуемо и согласовано.
Если α ≈ 0.5 → белый шум → хаос → команда не работает.
Если α ≈ 1.0 → розовый шум → баланс → команда выигрывает.
Если α ≈ 1.5 → красный шум → застой → команда сливает катку.
Да, ученые реально анализируют ЭЭГ игроков и голосовой чат через DFA.
И знаете что? У победителей — α близок к 1.0. То есть — розовый шум в голове и в микрофоне.
Вывод: красота в слаженности
Выигрывает не та команда, где все меткие.
Выигрывает та, где все в ритме.
Иногда случайная пятерка лосей становится симфоническим оркестром розового шума.
А сборная мира — белым шумом в микрофоне и красным в голове.
Что делать?
Перестаньте обвинять в каждом поражении.
Говорите по делу, без крика.
Меняйте тактику, если не работает.
Найдите в команде того, кто будет "ритмом" — даже без лучшего aim.
Старайтесь быть немного розовее.
Розовый шум — это и есть тот самый «красивый шум», который мы все ищем.
В музыке. В природе. В отношениях.
И да — даже на Dust2.
В написании поста немного помогла нейросеть Qwen
Нерешённые задачи школьной математики: проблема Гольдбаха – Алексей Савватеев | Лекции по математике
В чём заключается проблема Гольдбаха? Можно ли её доказать или опровергнуть? Какие есть успехи в её решении?
Наглядно показывает и рассказывает Алексей Савватеев, математик и матэкономист, доктор физико-математических наук, член-корреспондент РАН, популяризатор математики среди детей и взрослых, научный руководитель Кавказского математического центра АГУ, профессор Московского физико-технического института, ведущий научный сотрудник ЦЭМИ РАН.
День #10 Решил домашку из 4 семинара 1 части матана
Извините что грязно оформил. Потом научусь красиво делать посты))
0* я не стал решать))
Забыл, что препод по семинарам просил 42 б просто предложить выражение, а не решать уравнение, я заколебался с этим выражением
Я думал оно решается очень сложно, но по факту, если разделить на два множителя: 1) кубический корень из n^2 деленную на n+1
2) sin(n!)
Тогда мы сможем легко определить что первая часть стремится к 0, а вторая часть ограничена от -1 до 1. И у нас получается 0 * sin(n!), И ответ 0
Тоже просто решается оказывается. Надо всего лишь записать в виде суммы геом прогрессии, потом уже видно, что b^(n+1) и a^(n+1) стремятся к нулю и у нас полностью иcчезает n.
И ответ (1-b)/(1-a)
Вот ссылка с разбором:
Номер 53 практически сам решил. По кайфу. Лишь вспомнил о том, чему равна кубическая сумма. Но думаю чем больше я узнаю, тем меньше я буду заглядывать в подсказки.
Я конечно понимаю, что в пределе самый крайний член будет равен нулю и тогда все выражение будет равно нулю, так как каждый раз мы берем все меньшую часть единицы, но доказать это прям грамотно не смогу)
Можно конечно попытаться записать в виде 2n/2n - 1/2n но что нам это даст?
КАПЕЕЕЕЕЦ, чтАААААА
как так?
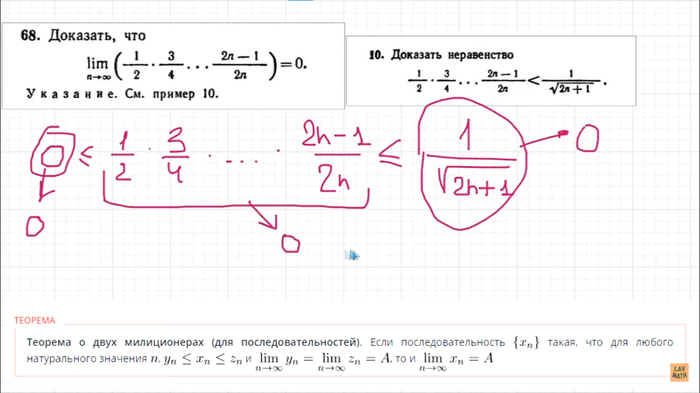
Короче вот так вот, живите теперь с этим. Так просто оказывается, он тупо взял его и между двумя нулями засунул и получил 0. Жесть
Дело в том, что мы ранее доказывали, что по индукции все это равно правой 1/корень(2n+1), а оно по своей сути стремится к 0. А наше выражение с огромным количеством множителей больше 0, поэтому мы все это выражение засунули между ними, и по теореме двух милиционеров получили что и он равен 0
Задача №57