Идея акторно-сетевой теории пришла из постструктуралистской семиотики. Семиотика (в европейском десоссюровском варианте синхронической лингвистики) показывает, что значение всякого слова относительно, то есть, конституировано отношениями различия между данным словом и другими связанными с ним словами. Например, слова «собака» и «кошка». Каждое из этих слов приобретает значение благодаря отличию от другого и каждое из них соотносимо с иными именами: «собака», «кошка», «волк», «щенок» и т.д. Значение слова произвольно (arbitrary), хотя и сильно детерминировано сетью отношений различия. По сути, оно представляет собой результат этих отношений.
Структуралисты, как правило, утверждают, что такая произвольная природа языка открывает нечто универсальное в операциях человеческого мышления. Люди структурируют отношения определенными способами и делают это посредством содержащейся в их головах машинерии.
Соответственно, предполагается, что все языки обладают одной и той же «глубинной структурой». В противоположность структуралистскому тезису об универсальности глубинной структуры, постструктурализм провозгласил существование различных, находящихся в процессе становления глубинных структур, создающихся и поддерживающихся в разных социальных ареалах. Данные структуры производят различные типы объектов и различные знания об этих объектах.
С точки зрения акторно-сетевой теории любой объект представляет собой сеть, причем сетевой анализ применим к различным уровням ее изучения. Например, на работе вы менеджер среднего звена покупаете у одних и продаёте другим, подписываете договора, получаете зарплату, на кого-то кричите и получаете выговор, вы вписаны в сеть социальных связей, хотя дома ваши близкие о них имеют слабое представление, для них вы брат, сват, муж, отец, а на улице вы вообще участник дорожного движения и никому и дела нет с кем вы подписываете договора или кому вы отец, главное чтобы не обочечник))
Кстати, тот же Эвергрин может быть представлен в виде сети технологического оборудования: корпус, движок, груз, каюты, команда; его навигационная система, со всеми ее эфемеридами, астролябиями и квадрантами, таблицами расчетов, картами, штурманами и звездами, также может быть рассмотрена как отдельная сеть. Весь его маршрут с его портами и пакгаузами, контрактами и контрагентами, рынками и покупателями может быть описана в тех же категориях.
Акторно-сетевой теории утверждает, что объект (например, корабль) остается объектом до тех пор, пока отношения между ним и связанными с ним объектами устойчивы и все сохраняется на своих местах. Штурманы, ветра и течения, команда, складские помещения, оборудование: если эта сеть сохраняет устойчивость, корабль остается кораблем, он не тонет, не превращается в щепки, напоровшись на тропический риф, не оказывается захваченным пиратами и уведенным в
Аравийское море. Корабль определяется своими отношениями с другими объектами, и
акторно-сетевой анализ направлен на исследование стратегий, которые производят (и, в свою
очередь, произведены) этой объектностью, синтаксисом или дискурсом, определяющими
место корабля в сети отношений.
Брюно Латур предложил интересную версию этой истории. Он говорит о неизменных мобильностях. Корабли представляют собой «мобильности», потому что действительно перемещаются из Лиссабона в Калькутту. А «неизменные» они потому, что сохраняют при этом перемещении свою форму как сетевые единства. Таким образом, сетевая метафора действует в двух направлениях, на двух уровнях анализа, упомянутых выше. Неизменные мобильности, будучи объектами, сами являются сетями, ансамблями отношений. Но они также включены в сеть отношений с иными объектами. Если эта сеть разрывается, корабль перестает быть кораблем, теряет свою сетевую форму, превращаясь во что-то другое.
Все вышесказанное – пример классического акторно-сетевого анализа. Менее привычна другая идея: конституирование объектов с необходимостью предполагает включение пространственных отношений. Латуровский термин «неизменные мобильности» отсылает к понятию движения – движения через пространство.
Топология – отрасль математики, изучающая характер объектов в пространстве. Как
она работает на практике? Нематематический ответ состоит в том, что топологи изучают
пространственность с точки зрения непрерывности фигур. Фигуры сохраняют свойство
непрерывности, даже будучи деформированными. В топологии, например, утверждается, что
фигура сохраняет непрерывность своей формы, если она сплющена, согнута или растянута,
но не в том случае, если она разорвана или сломана. При разрыве или повреждении
поверхности она трансформируется, то есть не является более гомеоморфной. Например,
топологически куб тождественен сфере, они гомеоморфны. Однако обе эти фигуры
принципиально отличаются от фигуры бублика, потому что бублик можно получить из шара
или куба, лишь проделав в них отверстие. В двумерном пространстве окружность и квадрат
гомеоморфны, но отличны от дуги – чтобы получилась дуга, линию, образующую
окружность (или квадрат), нужно разрезать.
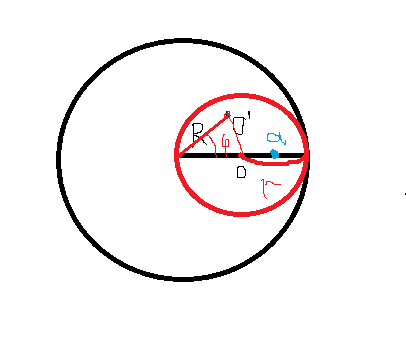
Пространство по характеру своему географично, евклидово, но это обманчивое ощущение, потому что евклидова геометрия описывает лишь одну из пространственных возможностей. Топологи создают и исследуют разные вероятные пространства или (что, впрочем, одно и то же) различные условия, в которых объекты могут быть деформированы без повреждений. Конвенциональный характер этого вопроса станет более очевидным, если мы обратимся к примеру. Представьте себе круг в круге- это Положение А. Мне лень рисовать поэтому я взял первую попавшуюся, не обращайте внимание на надписи))
Положение В эти два круга рядом, мне снова лень рисовать))
Топологически две эти формы не эквивалентны. Потому что если мы захотим преобразовать Положение А в Положение В, нам будет недостаточно одной лишь деформации. Нам придется разрезать большую окружность, чтобы вытащить меньшую «наружу». Следовательно, непрерывность большей окружности будет нарушена, а гомеоморфизм – потерян. Однако это верно лишь в том случае, если мы мыслим в двумерном пространстве и вынуждены проводить свои преобразования на плоскости. Если же мы не ограничены двумя измерениями, то достаточно перекинуть одну окружность через другую в точке их соприкосновения и Положение А будет преобразовано в Положение В без утраты гомеоморфизма. Непрерывность объекта не пострадает.
Приведенный пример иллюстрирует два интересующих нас аспекта проблемы: вопервых, он показывает, что пространственность – это конвенция; во-вторых, что для адекватного ее описания одной евклидовой геометрии мало6. Кроме того, пример с окружностями показывает, как тесно связаны между собой вопросы пространственности и непрерывности объектов. При каких обстоятельствах объект может быть изменен (например, перемещен в пространстве относительно прочих объектов) без трансформации его формы? Этим вопросом занимается топология как область математики, призванная исследовать способности различных фигур к трансформациям (и различные пространства, которые делают эти трансформации возможными).
Самой очевидной формой пространства является евклидово пространство. Фигура здесь мыслится как нечто помещенное в систему координат, образованную тремя ортогональными осями, а объект полагается неизменным, если его координаты в трехмерном пространстве остаются постоянными относительно друг друга. Изменение – например, перемещение объекта с одного места на другое, перемещение относительно других объектов – не означает утраты
гомеоморфизма, если только отношение координат остается прежним. Так, корабль остается
тем же самым кораблем, если, плавая по морям, сохраняет свою форму как физическое тело.
Однако акторно-сетевая теория работает с другой, гораздо менее очевидной формой
пространственности. Зададимся вопросом: что составляет непрерывность формы объекта как
сетевого единства? Объект остается тем же самым объектом, пока сохраняет свое место
в устойчивой сети отношений с другими вещами. Следовательно, ответ на данный вопрос:
стабильность порядка отношений. Чтобы можно было показать пальцем на объект и
сказать: «это корабль» (причем, корабль нормально функционирующий, а не застрявший в канале)
Обратите внимание: в евклидовом пространстве корабль есть устойчивая совокупность ортогональных координат, описывающих положение кормы, носа, киля относительно друг друга; пока корабль плывет, все эти части образуют единое целое. В пространстве сетей корабль также представляет собой устойчивый и непрерывный объект, «сетевую форму», целостность которой зависит от позиций всех релевантных, связанных с ним объектов. Так поддерживается объектная сущность судна. Это означает, что корабли пространственно или топологически множественны, т.е. находятся одновременно и в евклидовом пространстве и в пространстве сетевых отношений. Корабли гомеоморфны в каждом из пространств, поскольку сохраняют свою форму в обоих: физически – в одном, функционально или синтаксически – в другом. Однако перемещаются эти объекты лишь в евклидовом пространстве, в пространстве сетей они неподвижны. Никакого изменения отношений между компонентами, образующими корабли как объекты, не происходит. А если происходит, значит, что-то не так, значит их сетевая форма «разорвана». В то же время именно неподвижность корабля в сетевом пространстве
делает возможным его перемещение в пространстве евклидовом, позволяя ему без
повреждений покрывать расстояние между Калькуттой и Лиссабоном.
Нам свойственно ощущение «вечного евклидова пространства» – кажется, что пространство предшествует объектам и определяет условия их возможности. Мы чувствуем, что пространство появилось задолго до нас, что оно представляет собой нейтральный «контейнер», внутри которого нашим телам (или кораблям) приходится существовать. Отчасти это так. Без сомнения,
существуют отдельные пространственные конфигурации, предшествующие некоторым
объектам в евклидовом пространстве. Но, как мы отмечали выше, в топологии вопросы
пространственности и гомеоморфизма объектов неразрывно связаны. Действительно,
топологически объекты и пространства созданы вместе. Изобретая объекты и определяя, что
в их случае будет считаться неизменностью формы, топология вместе с тем изобретает и
определяет пространственные условия их возможности. Однако мы можем развить этот
аргумент и за пределами топологии. Объект из нашей повседневной жизни, сформированный, деформированный или перемещенный с сохранением непрерывности формы в евклидовом пространстве, в то же время создает это пространство.
С точки зрения здравого смысла такое утверждение неприемлемо в основном потому,
что мы не видим работы по производству пространства. Пространственность «осела» в
вещах. Если евклидово пространство воспринимается как вечное и неизменное, то
представление о пространстве как о пред-существующем контейнере кажется вполне
приемлемым. Поверить в создаваемость пространства трудно. Однако здесь – скорее
случайно, чем намеренно – акторно-сетевая теория может оказаться полезной. Представить
себе создание сети соотносимых друг с другом объектов гораздо легче, чем производство
евклидова пространства, уже хотя бы потому, что в производство объектов вовлечена более
или менее зримая инженерия, но нелепая случайность с Эвергрин доказывает нам что для корабля нужен маршрут, необходимы каналы, соответсвующие порты и инфраструктура. То есть
когда создается (сетевой) объект, создается также и весь (сетевой) мир, с его собственной пространственностью, собственным определением гомеоморфизма и непрерывности формы.
Однако это всего лишь первый шаг. Все гораздо сложнее, поскольку образование
сетевых пространств предполагает также производство евклидовой пространственности10.
Отчасти это вполне очевидный аргумент. Объекты (например, корабли), регионы (скажем,
страны), измерения расстояний (таких, как расстояние от Лиссабона до Калькутты)
произведены сетевыми средствами. Например, границы и расстояния произведены
исследователями, которые знали, как использовать теодолиты, чтобы измерить углы между
тригонометрическими точками, сделать аккуратную запись этих измерений, принести запись
в картографический центр, где на основе уже имеющихся измерений и с использованием
имеющихся навыков на двумерной поверхности была нарисована карта.
Топология создает пространства посредством установления правил, правила дают
ответ на вопрос «что именно следует считать гомеоморфным объектом?». Число возможных
правил (и, соответственно, возможных пространств) не ограничено. Акторно-сетевая теория
настаивает на пространственном понимании объектов и объектном понимании пространств,
населенных и созданных этими объектами. Отсюда напрямую следует отказ от реификации
евклидова пространства, указание на взаимное производство пространств и объектов.
Я хотел бы закончить свой текст утверждением: пространственные системы политически не нейтральны. Они являются политическими, потому что создают объекты и субъекты определенного вида и с определенным типом гомеоморфности. Потому что устанавливают пределы условиям возможности объектов. Потому что формулируют запреты на те или иные формы «инаковости». И потому что (как в случае с сетевым пространством) стремятся эти «инаковости» устранить. Сети, таким образом, воплощают и производят «политическое», замаскированное под «функциональное».